Cours : Espace vectoriel
 En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d'effectuer des combinaisons linéaires.
En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d'effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée +) munie d'une action compatible de K (voir la définition exacte). Les éléments de E sont appelés des vecteurs, et les éléments de K des scalaires.
Pour une introduction au concept de vecteur, voir l'article Vecteur.
On appelle K-espace vectoriel (ou espace vectoriel sur le corps K) tout ensemble E muni d'une loi interne « + » et d'une loi de composition externe à gauche « • », de K sur E, répondant aux critères suivants :
-
- (E,+) est un groupe abélien (commutatif) ;
- L'élément neutre du groupe (K,•) est neutre à gauche pour la loi « • » :

- la loi « • » est distributive à gauche par rapport à l'addition + de E :

- La loi « • » est exodistributive à droite par rapport à l'addition du corps K :

- La loi « • » est exo-associative par rapport à la multiplication du corps K (elle l'« importe » dans l'espace vectoriel) :
 .
.
Si  ou
ou  , on parle respectivement d'espace vectoriel rationnel, réel ou complexe. Cette terminologie s'utilise notamment en analyse.
, on parle respectivement d'espace vectoriel rationnel, réel ou complexe. Cette terminologie s'utilise notamment en analyse.
Dans certains ouvrages, les vecteurs peuvent être notés surmontés d'une flèche ou écrits avec des lettres en gras.
Notons que la condition d'exoneutralité :  peut sembler superflue ou évidente. Il n'en est rien. On peut en effet trouver un modèle de la théorie des espaces vectoriels dans lequel cette condition n'est pas satisfaite. Ceci prouve qu'elle ne se déduit pas des autres axiomes de la théorie. Et un tel modèle est en fait très facile à définir : il suffit de faire agir K sur K en posant, pour tous
peut sembler superflue ou évidente. Il n'en est rien. On peut en effet trouver un modèle de la théorie des espaces vectoriels dans lequel cette condition n'est pas satisfaite. Ceci prouve qu'elle ne se déduit pas des autres axiomes de la théorie. Et un tel modèle est en fait très facile à définir : il suffit de faire agir K sur K en posant, pour tous  et
et  ,
, 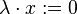 . Tous les axiomes sont satisfaits sauf l'exoneutralité puisque pour tout
. Tous les axiomes sont satisfaits sauf l'exoneutralité puisque pour tout  ,
,  .
.
Des axiomes ci-dessus découlent les propriétés suivantes :
- Un espace vectoriel étant un groupe, il est nécessairement non-vide.
- L'élément zéro « 0 » du corps K est exoabsorbant à gauche pour la loi • :

- L'élément neutre de l'addition vectorielle est absorbant à droite pour la loi • :
 .
.
Les deux opérations sur un espace vectoriel permettent de définir la combinaison linéaire, c'est-à-dire la somme finie de vecteurs affectés de coefficients (scalaires). La combinaison linéaire d'une famille de vecteurs  ayant pour coefficients
ayant pour coefficients  est le vecteur de E donné par :
est le vecteur de E donné par : 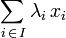 .
.
Lorsque l'ensemble d'indexation  est infini, il est nécessaire de supposer que le support de la famille
est infini, il est nécessaire de supposer que le support de la famille  (c'est-à-dire l'ensemble des indices i pour lesquels λi est non nul) soit fini.
(c'est-à-dire l'ensemble des indices i pour lesquels λi est non nul) soit fini.
La classe des espaces vectoriels n'est pas un ensemble. La classe des espaces vectoriels sur un corps fixé, même identifiés à isomorphisme linéaire près, n'est pas non plus un ensemble. De ce fait, la liste d'exemples suivante ne saurait être exhaustive.
- L'espace nul est l'espace vectoriel sur un corps K comportant un unique élément, qui est nécessairement le vecteur nul. L'espace nul est l'objet initial et l'objet final de la catégorie des espaces vectoriels sur K.
- Le corps K se présente comme un espace vectoriel sur lui-même : l'addition et la multiplication fournissent respectivement la loi interne et la loi externe.
Plus généralement, toute extension de corps de K, c'est-à-dire tout plongement de K dans un corps L, munit L d'une structure d'espace vectoriel sur K. - L'ensemble des translations d'un espace affine (par exemple le plan ou l'espace usuel) est un espace vectoriel.
- L'ensemble Kn des n-uplets d'éléments de K forme un espace vectoriel dans lequel l'addition se fait terme à terme et la multiplication par un scalaire est distribuée sur chaque terme.
Cette construction s'étend à l'espace vectoriel K∞ des suites à support fini. - Pour tout ensemble I, le produit quelconque KI est un K-espace vectoriel muni des lois d'addition terme à terme et de multiplication extérieure sur chaque terme :
- (Le vecteur nul est alors la famille de scalaires dont tous les termes sont nuls.)
-
- Lorsque I est le produit cartésien
![[[1 ; n]]\times[[1 ; p]]](http://upload.wikimedia.org/math/0/8/c/08c275ddf5afd14e77daa8e5669f73fa.png) , ce produit est l'espace vectoriel
, ce produit est l'espace vectoriel 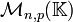 des matrices à n lignes et p colonnes à coefficients dans K.
des matrices à n lignes et p colonnes à coefficients dans K.
- Plus généralement, le produit quelconque d'une famille (Ei ) d'espaces vectoriels sur K est un espace vectoriel sur K qui se note
 . (Il s'agit du produit des espaces vectoriels au sens des catégories.)
. (Il s'agit du produit des espaces vectoriels au sens des catégories.)
- L'ensemble des familles à support fini
 forme aussi un espace vectoriel, appelé la somme directe des espaces Ei et qui se note
forme aussi un espace vectoriel, appelé la somme directe des espaces Ei et qui se note  .
.
- L'ensemble
 des fonctions continues réelles ou complexes définies sur espace topologique X est un espace vectoriel (réel ou complexe).
des fonctions continues réelles ou complexes définies sur espace topologique X est un espace vectoriel (réel ou complexe). - L'ensemble des (germes de) solutions d'une équation différentielle linéaire homogène est un espace vectoriel (réel ou complexe).
- L'ensemble des suites numériques satisfaisant une relation de récurrence linéaire est un espace vectoriel.
Un sous-espace vectoriel d'un espace vectoriel E est un sous-groupe additif F de E stable par l'action de K, c'est-à-dire tel que :
- l'élément zéro 0 appartient à F ;
- la somme de deux éléments de F est un élément de F ;
- l'inverse d'un élément de F pour la loi additive est un élément de F ;
- le produit d'un scalaire par un vecteur de F appartient à F.
De manière équivalente, un sous-espace vectoriel est une partie non vide et stable par combinaison linéaire.
Par exemple, l'ensemble des fonctions polynômes réelles est un sous-espace vectoriel de l'espace vectoriel  des fonctions continues sur
des fonctions continues sur  .
.
L'intersection de deux sous-espaces vectoriels est un sous-espace vectoriel mais l'union n'en est pas un en général. C'est pourquoi on définit la somme de deux sous-espaces vectoriels F et G comme l'ensemble
-
 .
.
Cette somme est un sous-espace vectoriel. C'est même le plus petit sous-espace vectoriel (au sens de l'inclusion) contenant les deux sous-espaces vectoriels initiaux.
Deux sous-espaces vectoriels F et G de E sont dits en somme directe lorsque leur intersection est l'espace nul. Leur somme est alors notée  .
.
On dit que les sous-espaces vectoriels F et G sont supplémentaires (l'un de l'autre) dans E s'ils sont en somme directe et si  . L'axiome du choix permet d'assurer l'existence d'un supplémentaire à tout sous-espace vectoriel, mais il n'y a jamais unicité (sauf dans le cas du sous-espace nul ou de l'espace total). Par exemple, dans
. L'axiome du choix permet d'assurer l'existence d'un supplémentaire à tout sous-espace vectoriel, mais il n'y a jamais unicité (sauf dans le cas du sous-espace nul ou de l'espace total). Par exemple, dans  , les supplémentaires d'un plan vectoriel quelconque sont toutes les droites vectorielles non contenues dans ce plan. Il existe donc ici une infinité de supplémentaires différents.
, les supplémentaires d'un plan vectoriel quelconque sont toutes les droites vectorielles non contenues dans ce plan. Il existe donc ici une infinité de supplémentaires différents.
Si E est la somme directe de F et G, tout vecteur de E se décompose alors de manière unique en une somme de deux vecteurs, l'un appartenant à F et l'autre à G. Plus généralement, une famille de sous-espaces vectoriels (Fi) est dite en somme directe dans E si tout vecteur de E s'écrit de manière unique comme une somme  avec pour tout i,
avec pour tout i, 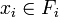 . Cette définition implique que les sous-espaces vectoriels Fi soient d'intersection nulle deux à deux et que leur somme soit égale à E mais la réciproque est fausse. Il suffit de prendre comme contre-exemple dans le plan
. Cette définition implique que les sous-espaces vectoriels Fi soient d'intersection nulle deux à deux et que leur somme soit égale à E mais la réciproque est fausse. Il suffit de prendre comme contre-exemple dans le plan  les trois droites dirigées par
les trois droites dirigées par  ,
, 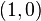 et
et 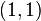 .
.
Soient  et
et 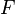 deux espaces vectoriels. Une application
deux espaces vectoriels. Une application 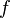 de
de  dans
dans 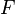 est dite linéaire si elle préserve les combinaisons linéaires, c'est-à-dire :
est dite linéaire si elle préserve les combinaisons linéaires, c'est-à-dire :
-
 .
.
L'ensemble des applications linéaires de E dans F est noté L(E,F). Lorsque  , ces applications sont appelées endomorphismes de E et on note leur ensemble L(E).
, ces applications sont appelées endomorphismes de E et on note leur ensemble L(E).
Un isomorphisme d'espaces vectoriels est une application linéaire bijective. Un automorphisme est un endomorphisme bijectif. L'ensemble des automorphismes de E est le groupe linéaire noté 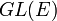 .
.
On peut citer les exemples suivants d'applications linéaires.
- L'application nulle est le neutre pour l'addition vectorielle dans L(E,F).
- L'application identité et plus généralement toutes les homothéties vectorielles (non nulles) sont des automorphismes.
- Les symétries, rotations et similitudes vectorielles (non nulles) sont des automorphismes du plan ou de l'espace usuel.
- Les projecteurs sont des endomorphismes.
- La dérivation est un endomorphisme de l'espace vectoriel des polynômes.
Une forme linéaire sur un K-espace vectoriel E est une application linéaire de E dans K.
L'ensemble des formes linéaires sur E est appelé l'espace dual de E et il est noté E*.
Soit  .
.
- On appelle noyau de
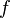 et on note
et on note  l'ensemble
l'ensemble  .
. - On appelle image de
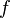 et on note
et on note  l'ensemble
l'ensemble 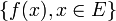 .
.
On a les propriétés suivantes :
- L'image et le noyau sont des sous-espaces vectoriels respectivement de l'espace but et de l'espace source.
- Une application linéaire est injective si et seulement si son noyau est l'espace nul.
- L'ensemble L(E,F) est un espace vectoriel.
- L'espace vectoriel
 s'identifie à l'espace des matrices
s'identifie à l'espace des matrices 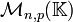 .
.
Soit F un sous-espace vectoriel de E. L'espace quotient E/F (c'est-à-dire l'ensemble des classes d'équivalence de E pour la relation « u~v si et seulement si u-v appartient à F», muni des opérations définies naturellement sur les classes) est un espace vectoriel tel que la projection  (qui associe à u sa classe d'équivalence) soit linéaire de noyau F.
(qui associe à u sa classe d'équivalence) soit linéaire de noyau F.
Un sous-espace vectoriel G de E est un supplémentaire de F si et seulement si la restriction de la projection induit un isomorphisme de G sur E/F.
Famille de vecteurs et dimension [modifier]
Une famille  d'éléments de E est dite libre (sur
d'éléments de E est dite libre (sur  ) lorsque toute combinaison linéaire d'éléments de
) lorsque toute combinaison linéaire d'éléments de  à coefficients non tous nuls est non nulle, autrement dit lorsque la seule combinaison linéaire nulle d'éléments de
à coefficients non tous nuls est non nulle, autrement dit lorsque la seule combinaison linéaire nulle d'éléments de  est celle dont tous les coefficients sont nuls. Dans ce cas les vecteurs de cette famille sont dits linéairement indépendants (les uns des autres).
est celle dont tous les coefficients sont nuls. Dans ce cas les vecteurs de cette famille sont dits linéairement indépendants (les uns des autres).
Au contraire, une famille d'éléments de E est dite liée lorsqu'elle n'est pas libre, c'est-à-dire s'il existe une combinaison linéaire nulle des éléments de cette famille à coefficients non tous nuls (c'est ce qu'on appelle une relation de dépendance linéaire).
Par exemple, une famille d'un seul vecteur non nul est toujours libre. A contrario, une famille quelconque comportant le vecteur nul est toujours liée.
On montre qu'une famille  de deux vecteurs de E est liée si et seulement s'il existe un scalaire
de deux vecteurs de E est liée si et seulement s'il existe un scalaire  tel que
tel que  ou un scalaire
ou un scalaire 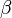 tel que
tel que 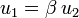 . On dit dans ce cas que les deux vecteurs sont colinéaires. En revanche, rien n'assure qu'une famille liée comportant au moins trois vecteurs contienne forcément deux vecteurs colinéaires.
. On dit dans ce cas que les deux vecteurs sont colinéaires. En revanche, rien n'assure qu'une famille liée comportant au moins trois vecteurs contienne forcément deux vecteurs colinéaires.
Une famille d'éléments de E est dite génératrice (de E) lorsque tout élément de E peut s'exprimer d'au moins une manière sous la forme d'une combinaison linéaire des éléments de cette famille.
On appelle base de l'espace vectoriel E toute famille d'éléments de E libre et génératrice.
L'intérêt des bases réside dans les propriétés suivantes :
- Une famille
 d'éléments de E est une base si et seulement si tout élément u de E s'exprime de manière unique comme combinaison linéaire des éléments de
d'éléments de E est une base si et seulement si tout élément u de E s'exprime de manière unique comme combinaison linéaire des éléments de  .
. - Le choix d'une base pour un K-espace vectoriel permet d'identifier celui-ci avec une puissance de K et, si cette base est finie, d'utiliser les matrices pour représenter des applications linéaires.
Pour un espace vectoriel donné, l'existence d'au moins une base est assurée en toute généralité par l'axiome du choix. Cependant, on peut se dispenser de cette hypothèse lorsqu'il existe une famille génératrice finie (ou indexée par un bon ordre).
Si un K-espace vectoriel E admet une base ayant un nombre fini d d'éléments, alors toute base de E a ce même cardinal d.
L'entier d est appelé la dimension de E, notée  ou, s'il n'y a pas d'ambiguïté,
ou, s'il n'y a pas d'ambiguïté,  . On dit alors que E est un espace vectoriel de dimension finie (sur K), égale à d.
. On dit alors que E est un espace vectoriel de dimension finie (sur K), égale à d.
En particulier l'espace nul, ayant une base vide, est de dimension finie égale à 0.
On appelle droite vectorielle tout espace vectoriel de dimension finie égale à 1 et plan vectoriel tout espace vectoriel de dimension finie égale à 2. Un hyperplan est un sous-espace vectoriel de dimension n-1 dans un espace vectoriel de dimension n.
Si une application linéaire f a une image de dimension finie, cette dimension est appelée rang de f et se note 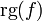 .
.
Un espace vectoriel E est de dimension finie si et seulement s'il admet une famille génératrice ayant un nombre fini d'éléments.
Les espaces vectoriels qui ne sont pas de dimension finie sont dits de dimension infinie C'est le cas notamment des espaces vectoriels de polynômes, les espaces de suites et plus généralement les espaces de fonction.
Pour qu'un espace vectoriel E soit de dimension infinie, il faut et il suffit qu'il existe une famille libre infinie d'éléments de E.
Soit E un espace vectoriel de dimension finie (non nulle) égale à n.
- Toute famille génératrice de E a au moins n éléments. Si une famille génératrice de E a n éléments, c'est une base de E (on dit que les bases sont les « familles génératrices minimales »).
- Toute famille libre de E a au plus n éléments. Si une famille libre de E a n éléments, c'est une base de E (on dit que les bases sont les « familles libres maximales »).
- Le théorème de la base incomplète stipule que si
 est une famille libre de vecteurs de E telle que
est une famille libre de vecteurs de E telle que  (autrement dit, une famille libre qui n'est pas une base puisqu'elle n'est pas maximale), alors il existe n – p vecteurs de E, qu'on peut noter
(autrement dit, une famille libre qui n'est pas une base puisqu'elle n'est pas maximale), alors il existe n – p vecteurs de E, qu'on peut noter  , tels que la famille
, tels que la famille 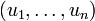 soit une base de E.
soit une base de E.
- Tout sous-espace vectoriel F de E est de dimension finie, et dim F ≤ dim E.
- Si F est un sous-espace vectoriel de E tel que dim F = dim E, alors F = E.
- Si F1 et F2 sont deux sous-espaces vectoriels de E, alors
 .
. - Cette relation est connue sous le nom de formule de Grassmann.
- Tous les supplémentaires d'un sous-espace vectoriel F de E ont la même dimension, qui est appelée codimension de F dans E.
- L'espace dual de E est également de dimension finie et
 .
. - Tout hyperplan de E est le noyau d'une forme linéaire non nulle sur E.
- Soit
 une base de E.
une base de E.
- Il existe une unique base
 de
de 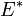 telle que
telle que  ,
, - où
 est le symbole de Kronecker.
est le symbole de Kronecker. - On dit alors que
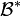 est la base duale associée à
est la base duale associée à 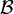 .
.
- L'ensemble des formes n-linéaires alternées sur un espace vectoriel de dimension n est un espace vectoriel de dimension 1. Ce résultat est à la base de la théorie du déterminant.
- Si f est une application linéaire f de E dans un espace vectoriel F (non nécessairement de dimension finie), alors f induit un isomorphisme de tout supplémentaire de
 dans
dans  .
.
- Cette propriété permet de démontrer le théorème du rang :
-
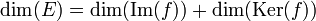 , autrement dit
, autrement dit  .
.
- Le rang est la dimension de l'espace des colonnes, qui est égale à celle de l'espace des lignes
/image%2F1492414%2F20171125%2Fob_4e99b6_xibniy.jpg)



/image%2F1492414%2F20210221%2Fob_a4adc0_amille.jpg)
/image%2F1492414%2F20210221%2Fob_3296ce_afrique.jpg)
/image%2F1492414%2F20210126%2Fob_024817_at.jpg)
/image%2F1492414%2F20210126%2Fob_650c8e_a3.jpg)
