Les nombres : Histoire et évolution - Ibni
L'humanité a mis des millénaires pour passer de la quantité aux nombres. L'idée de nombre est l'aboutissement d'un long travail d'abstraction de la pensée.
| -30 000 | Présence d'entaillesnumériques. |
|---|---|
| - 8 000 | Apparition descalculi au Moyen Orient. |
| -3 300 | Premiers chiffres à Sumer et en Elam. Premièrenumérotation écrite. |
| -2 700 | Chiffres sumériens cunéiformes. |
| -2 000 | Apparition de labasedécimale. |
| -1 800 | Numérotation babylonienne savante. Première numérotation de position. |
| -1 300 | Apparition des chiffres chinois |
| - 6 ème siècle | Découverte des valeurs irrationnelles. Pythagore. |
| - 4 ème siècle | Première crise du concept d'infini. Aristote. |
| - 300 | Numérotation alphabétiquegrecque. |
| - 3 ème siècle | Apparition du premier zéro de l'histoire dans la numérotation savante babylonienne. |
| - 2 ème siècle | Numérotation de position chinoise sans zéro. |
| Premiers siècles apr. J.-C. | Les nombres négatifs. |
| 4/5 ème siècles | Numérotation de position indienne. |
| 5/9 ème siècle | Numérotation de position maya avec unzéro. |
| fin 8 ème siècle | Arrivée du calcul indien à Bagdad. |
| 10 ème siècle | Chiffre ghobar dans le Maghreb et dans la péninsule ibérique. |
| 12/15 ème siècle | Présence du zéro de la numérotation indienne en Occident. |
| 13 ème siècle | Premier usage d'une suite. Fibonaci. |
| 16 ème siècle | Premier emploi systématique des fractions continues.Bombelli. |
| 16 ème siècle | Invention de la notation littérale parViète. |
| 1635 | Les valeurs infinitésimales. Cavalieri. |
| 1677 | Invention du calcul infinitésimal parNewtonetLeibniz. |
| 1797 | Découverte d'une interprétation géométrique des nombres complexes parGauss. |
| 1825 | Découverte des nombres algébriques, ne pouvant pas s'exprimer par radicaux.Abel. |
| 1843 | Invention des quaternions.Hamilton. |
| 1844 | Découverte des nombres transcendants parLiouville. L'expression "transcendant" est cependant deLeibniz(17e) |
| Les marques numériques les plus anciennes dates des premières civilisation du Paléolithique (30 000 ans environ av. J.-C.). Le hommes, qui durent apprendre à conserver les nombres, avaient à leur disposition deux supports privilégiés, les os et le bois. | Bois de renne entaillé datant du Paléolithique |
>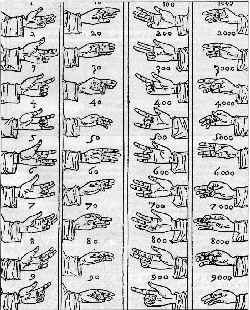 | Pour assurer cette fonction de mémorisation de la quantité, l'homme, hormis l'os, le bois ou la pierre, a aussi utilisé son propre corps (doigts, orteils, bras, jambes, articulations..). De nombreuses civilisation ont ainsi développé de complexes "cartographie corporelles numériques" accompagnées de grammaires gestuelles. Document tiré de la Summa arithmética de Luca pacioli |
Font ensuite leur apparition. Chaque nombre est représenté par un signe physique. Des marques sur un support "en dur" ou bien, des objets (cailloux, perles, coquillages, nœud, ficelles..) représentent donc des nombres et toutes sortes de dispositifs matériels ont été mis au point : calculi, tables à compter, "planches à poussière", abaques, bouliers, cordelettes à nœuds (présentes dans la Perse de Darius au 5èmesiècle av. J.-C.)
C'est en Mésopotamie et dans d'autres lieux du Moyen Orient (vers -8 000) qu'apparaissent lescalculi.
Dans la pratique, chaque caillou vaut "un" et pour des raisons de commodité évidente, on eut l'idée de remplacer un tas par un seul caillou de nature différente, par sa couleur ou par sa forme.
On retrouve d'ailleurs en Mésopotamie chez les sumériens des objets fabriqués ("pierres d'argile"), lescalculi(calculus, "caillou" en latin), dès la moitié du 4ème millénaire av J.-C.
C'est en Mésopotamie et dans d'autres lieux du Moyen Orient (vers -8 000) qu'apparaissent les calculi.
Dans la pratique, chaque caillou vaut "un" et pour des raisons de commodité évidente, on eut l'idée de remplacer un tas par un seul caillou de nature différente, par sa couleur ou par sa forme.
On retrouve d'ailleurs en Mésopotamie chez les sumériens des objets fabriqués ("pierres d'argile"), les calculi (calculus, "caillou" en latin), dès la moitié du 4ème millénaire av J.-C.
  | Dans la numérotation sumérienne, qui est de base 60, le petit cône vaut 1, la bille 10, le grand cône 60, le grand cône perforé 3600 et la sphère perforée 36 000. |
Tous ces dispositifs matériels souffrent d'une grande faiblesse, ils sont impuissant à garder trace du passé car chaque étape du calcul supprime les précédentes.
A Sumer, vers 3 300 av. J.-C., en Mésopotamie est née l'écriture. Elle aurait été élaborée pour la gestion de l'empire, terres, troupeaux, hommes, grains...
La première numérotation écrite est sumérienne. Dans les premières tablettes d'argile (qui nous ont révélé l'écriture), apparaissent des nombres. Numération écrite et écriture semblent être contemporaines.
 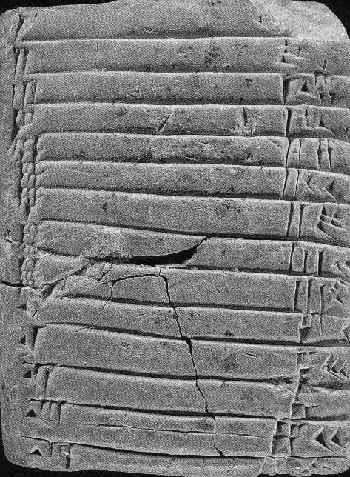 | A gauche , une tablette d'argile (2 400 ans av. J.-C.) en écriture cunéiforme où figurent clous et chevrons qui serons les chiffres de cette numération. A droite, une table de multiplication par 25, provenant de Suse et conservée au musée du Louvre (datant de -2 000 environ). |
L' établissement d'une comptabilité, devenue de plus en plus complexe, a nécessité un enregistrement des comptes. Ainsi serait née la première numérotation écrite (qui est sumérienne)
Les chiffres sont le plus souvent représentés par des symboles particuliers ("la fleur de lotus" par exemple en Égypte) mais quelques civilisations choisissent de ne pas en créer (la numérotation écrite hébraïque par exemple oula grecque-l'alpha est 1, bêta 2..- ).
Les règles de construction des numérotation écrite sont simple :
- il faut permettre une lecture sans ambiguïté, une même écriture ne devant pas représenter deux nombres différents.
- Il faut représenter un maximum de nombres avec un minimum de symboles.
C'est l'usage d'une base qui permettra de répondre au mieux aux contraintes posées.
Au lieu de compter uniquement par unités, on compte "par paquets".
La plus fréquente est la base décimale (10), mais on trouve également des bases sexagésimale (60), utilisée par les Sumériens, vicésimale (20), utilisée par les Mayas, duodécimale (12), quinaire (5), utilisée aussi par les Mayas et binaire (2).
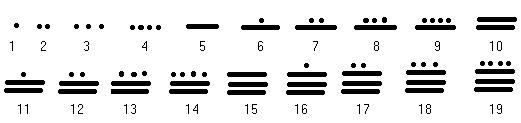
Chez les Mayas, le moyen le plus simple pour représenter les nombres était un système utilisant, le point valait 1, la barre 5 et un zéro. On les trouve sur le codex de Dresde.Dans leur base 20 de type additif, l'unité est représentée par un point, la vingtaine par une hache, le nombre 400=20*20 par une plume.
 |
| Ce document chiffre le tribut en nature payé par 7 villes aztèques aux seigneurs espagnols de Mexico.) |
-
Les différents types de numération
Ainsi, chaque numérotation va devoir de donner ses différentes unités (unité de premier ordre et puissances successives de la base).Les Égyptiens, les Chinois et les Grecs se sont successivement offert 3 numérations, les Mayas 2 et les Indiens 4.
Les Aztèques, Éthiopiens, Hébreux et Romains ont eu les leurs.On classe les différentes numérations en 3 groupes : (selon les opérations arithmétiques utilisées pour composer les nombres à partir des chiffres).
- numérations additives
- numérations de position
- numérations hybrides
- Numérations additives
Dans ces numérations, l'addition est la seule opération utilisée. La valeur d'un nombre est la somme des valeurs des symboles qui le composent.
Par exemple, dans la numération romaine, le I vaut "un" où qu'il se trouve dans l'écriture.
"mille un" s'écrit MI et "cent" s'écrit C.
La longueur du nom est donc sans rapport avec sa valeur. (ex MI "mille un" et DCCCLXXXVIII "888").
Remarques: La numération romaine n'est pas alphabétique. Les 7 symboles numériques - I, V, X, L, C, D, M- ne sont pas des lettres de l'alphabet latin. ce n'est qu'après un longue évolution qu'ils ont été assimilés à des signes alphabétiques.
Voir aussi la numérationgrecque.
Un problème évident se pose avec ce type de numération, comment écrire des nombres très grands ?
- Numérations hybrides
Ces numérations utilisent conjointement l'addition et la multiplication.
"deux cents" est conçu comme "deux" fois "cents" et représenté par "deux" suivi de "cent"
Mais chaque puissance de la base est représentée par un symbole différent, ce qui rend évident la faiblesse de ce principe pour représenter des nombres très grands.
- Numérations de position
Hormis la numération indienne qui est développée ci-après, il y eut à trois reprises, et de façon indépendante, création d'une numérotation de position.
- A Babylone, vers - 1 800.
- En Chine, au cours du 1er siècle avant notre ère.
- Dans l'empire Maya, entre le 5e et le 9e siècle.
Ces 3 numérations souffrent de la même faiblesse, la non indépendance des représentations des unités. Le "2" par exemple, n'est pas un chiffre spécifique, mais une itération du "1".
- L'invention de cette numération dans l'Inde au 5e siècle.
Les chiffres de "un" à "neuf" ont été inventés en Inde avant notre ère. Ils apparaissent dans des inscriptions de Nana Ghât au 3e siècle av.J.-C., mais le principe de position n'y est pas appliqué.La numération de position avec un zéro (qui était un point à l'origine), a été inventé au cours du 5e siècle. Dans un traité de cosmologie écrit en sanscrit en 458, le "LOKAVIBHAGA", "les parties de l'univers", on voit apparaître le nombre 14 236 713 écrit en toute lettres ( "un" "quatre" ...). dans ce texte, on trouve aussi le mot "sunya", "le vide", qui représente le zéro.C'est à ce jour le document le plus ancien faisant référence de cette numération.
- Propagation de cette numération
En 773, arriva à Bagdad une ambassade indienne avec un présent pour le calife MANSOUR et les savants arabes qui l'entouraient : le calcul et les chiffres.
Muhammad ibn Musa al-Khuwârizmia écrit le premier ouvrage en langue arabe présentant la numération indienne de position au 9e siècle, "livre de l'addition et de la soustraction d'après le calcul des Indiens". C'est par cet ouvrage que le calcul indien pénétra dans l'Occident chrétien. Maintes fois traduit en latin à partir du 12e siècle, sa célébrité fût telle que ce calcul fut nommé algorisme, d'Algorismus latinisationd'al-Khuwârizmi. Au Xe siècle, le moine françaisGerbert d'AURILLACapprit la nouvelle numération chez les Maures d'Espagne et, grâce aux chaires qu'il occupa dans les établissement religieux d'Europe, il put introduire le nouveau système en occident. En 999, il fut élu pape sous le nom deSYLVESTRE II, ce qui lui conféra l'autorité nécessaire pour implanter la numération indo-arabe. Certes une évolution s'ensuivit dans la comptabilité, les marchands ayant rapidement adopté les nouveaux chiffres, mais les mathématiques européennes n'y trouvèrent pas un sang neuf ! retour
- Abacistes contre algoristes et l'utilisation du zéro
Durant le haut Moyen Age, en Occident chrétien, les opération s' effectuaient sur des abaques (sortes de tables à colonnes), les chiffres étant inscrits sur des jetons, les apices.Raoul de Laon, un abaciste eut l'idée de placer dans les colonnes vides un caractères nommé sipos, "jeton", qui fût ensuite remplacé par le signe "0".
L'origine de "zéro": Çunya signifie vide en sanskrit, le zéro est représenté par un petit rond (Pourquoi un rond ? On ne le sait pas vraiment). Traduit en arabe, çunya devient sifr qui, traduit en italien, donna zéfiro. Et de zéfiro à zéro....( cf. aussi,le zéro)
Par la suite, ces abaques furent remplacées, non sans mal, par des "planches à poussières" utilisées par les algoristes, adeptes et utilisateurs du nouveau calcul venu du monde arabe.
On se trouve alors en présence d'un veto ecclésiastique et d'une levé de boucliers de la part de la caste des calculateurs professionnels. Veto qui sera maintenu, en divers endroits, jusqu'au 15e siècle (soit 5 siècles aprèsGerbert d'AURILLAC!!! c.f. ci-avant).
L'église était contre une démocratisation du calcul qui entraînerait sûrement pour elle la perte de son monopole en matière d'enseignement, et par conséquent, une perte de pouvoir.Les chiffres arabes demeurent donc, pour un temps, frappés d'interdit
| Les chiffres de "un" à "neuf" ont été inventés en Inde avant notre ère. Ils apparaissent dans des inscriptions de Nana Ghât au 3e siècle av.J.-C., mais le principe de position n'y est pas appliqué. La graphie de "nos" chiffres vient des Arabes occidentaux de l'Espagne maure. On les appelle les chiffres du ghobar. Le chemin emprunté fût long et dura environ 800 ans !: Inde-Moyen-Orient arabe-Afrique du Nord-Espagne maure. |
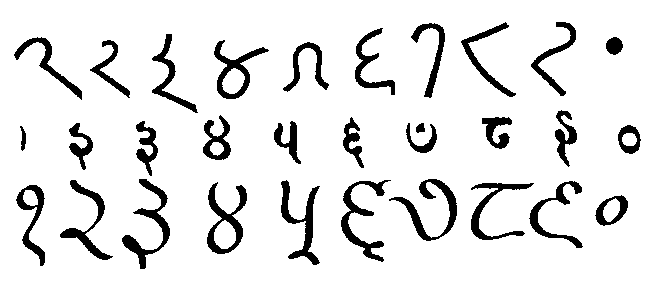 |
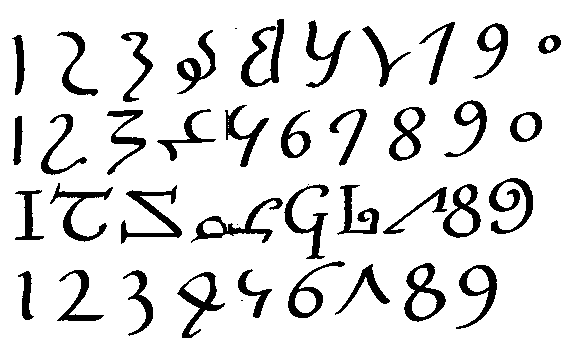 |
| Dans ce manuscrit indien du 12e siècle (cliquer sur l'image pour l' agrandir) figure le nombre 109 305. Le zéro est représenté par un point, le "bindu". |
 |
/image%2F1492414%2F20171125%2Fob_4e99b6_xibniy.jpg)



/http%3A%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2Fthumb%2F5%2F53%2FWalk2d_0.png%2F350px-Walk2d_0.png)
/http%3A%2F%2Fwww.math93.com%2Fimages%2Fimages_doc%2Fchasse-aux-tresors-mathematiques.jpg)
/http%3A%2F%2Fthumbs.dreamstime.com%2Fx%2Fnumber-zero-14039152.jpg)
/http%3A%2F%2Fwww.les-mathematiques.net%2Fphorum%2Ffile.php%3F2%2Cfile%3D1948%2Cin_body_attachment%3D1)
